|
Brick Siding In an age of artificial materials there is something very natural about brick siding. It is made of earth and reflects earth tones. It has earth solidity.
 Brick offers a richness and intricacy few other sidings can approach
Brick siding, like all forms of masonry, is timeless in its utility. It has no end-date. A lifetime warranty is a short span for a brick. They should come with a multi-generational warranty. Yet bricks can also be beautiful. They offer variety in form, color and texture, if you choose to take full advantage of their natural qualities.
If you want brick siding for your house you have four basic options. 1) You can go with a true brick wall. 2) You can use a brick veneer. 3) You can use some sort of artificial brick panels, similar to siding. 4) You can stamp a brick pattern into a lightweight cement overlay, similar to stucco. Each of these will be addressed in individual articles. This article will deal with true brick walls and with bricks in general. A Short Course on Bricks Bricks are simply made from fired clay. Back in the day they were made from whatever local clay was available and were the color of the local landscape. Today they are likely to be produced far away and the natural color will be altered with pigment to whatever color is specified by the homeowner or architect. It would be somewhat better for the environment if the bricks were produced on site from local clay. However the local clay is not always the best material. While many old bricks have withstood the ages, some have crumpled with time. Bricks produced today are made with more consistent controls over the quality of the materials and the forming process, so that homeowners have some assurance that their bricks will outlast their homes. Bricks are laid in rows, or courses, with mortar between each brick and between each course. The mortar is made from sand, lime and Portland cement. Let us consider the simplest wall first. The simplest wall is composed of bricks laid lengthwise. This gives a wall one brick wide, also known as a wythe. As you start to lay the second course of brick you quickly realize that you have a choice. You can simply stack the bricks so that each brick on the second course lines up with the brick below it. If you were to lay the bricks without mortar it would be obvious that such an arrangement would end up with a bunch of individual stacks of bricks that would be unstable. With mortar gluing the bricks together you could get by with such an arrangement, but in days past the mortar was always much weaker than the brick, so you would run the risk of cracks forming in the mortar and your individual stacks falling over. To counter this problem bricklayers stagger the bricks. Now there is no single seam running from top to bottom. Laying many such courses of bricks together provides you with the simplest bond, or pattern, the stretcher bond, also known as the running bond.  A stretcher bond has the stretcher face exposed on every brick. In most cases the bricks are centered on the gap between the bricks on the course below. In some variations the bricks are offset so that the gap between the bricks hits ¼ or 1/3 the way down the brick.
The name comes from one of the faces of the brick. If you look at typical brick it is longer than it is wide, and wider than it is tall. There are three pairs of faces. You might think that each face pair would have a name. No, its not that simple. Here is a graphic that might help explain the terminology. 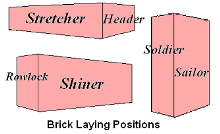 Each face has two names, depending on its exposed position.
The names of the faces change based on the orientation of the brick. A stretcher face is known as a soldier when the brick stands on end. A header becomes a rowlock. A shiner becomes a sailor. Why? I have no idea. It is just the way it developed. Now, the problem with a wall formed of one wythe of stretcher bond is that it isn’t very stable, and it isn’t very strong. It will tend to buckle, especially if it is supporting a lot of weight. If it is simply siding, and not bearing any weight, you can get by with this. However, if it is actually a structural wall you need more stability than a single wythe offers. To counter this problem builders long ago figured out that they needed wider walls. You could just run two wythes of stretcher bond side by side and connect them with mortar, but remember that mortar is weaker than brick. To keep one wythe from buckling and pulling away from the other wythe builders started laying some bricks so that they spanned the two wythes. This meant that some bricks presented the stretcher face and some presented the header face. There are multiple ways that this could be done, each creating its own visual pattern that can add interest to a wall.  A Flemish bond has every other brick showing the header. Many people consider this the most beautiful bond.
Other bonds have become popular at various times and places. I have inserted a few photographs with some explanation of several of these bonds.  American bond. It is still popular. It is mostly stretcher courses interspersed with courses of headers. The ratio of stretcher courses to header courses varies, but 5 to 1 is common.
 Here is the English bond. A stretcher course is followed by a header course.
 The Rat Trap bond is similar to the Flemish bond, but the shiners and rowlocks are used instead of stretcher and header. This means each wythe is narrower, with a small air gap between the wythes.
 Header bond. Like the stretcher bond, but sideways.
The stretcher bond is the most common bond seen today for the simple reason that most brick walls are only brick siding, a facing. They are tied in to a block or concrete or wood wall, and so they are only one brick thick. To me this reliance on the stretcher bond defeats the purpose of using brick siding. If you are going to use brick because of its pleasing appearance why use it in the manner that is least pleasing?
Decorative Brick Siding A pleasing bond allows the homeowner to create pleasing textures and patterns over the entire surface area of their house, but they may also choose to add decorative courses of bricks or special brick patterns in select areas. Just look at some of the beautiful patterns created in ages past, when brick siding was the preferred covering for a house. Polychromatic Brick Siding  Pixelated artistry in the medium of brick
In this example it appears that either the white and black bricks at the top were simply painted on, or actual tile was applied on top of the red background bricks as the white “bricks” begin right in the middle of some of the red bricks. However most of this appears to be genuine, fancy brickwork, varying the size of the bricks and the faces presented and using tinted bricks.
Depth and Bas Relief Bricks can be laid so that their faces are not all on the same plane. Bricks can be indented or partially pulled out from the wall so that a three-dimensional surface is created. You can also lay them at an angle so that corners are exposed. Three-dimensional brick siding has the added advantage of changing its appearance throughout the day as the sun creates a shifting pattern of shadows. This simple checkerboard pattern is comprised of a headers stacked with every other brick indented. The indentations create shadows and the shadows change throughout the day. Like many cities, the old neighborhoods of Washington, D.C. are filled with brick houses built in a day when developers weren’t afraid of ornamentation. Simple devices like this checkerboard made each house and neighborhood a little different. The brick siding was used to distinguish what were otherwise identical houses
 Bricks can be both ornamentation and structural. Brick siding gives the opportunity to define the space more than other forms of siding.
Stringer courses A projecting course that runs horizontally around a building, or along one wall. This is often used to highlight the division between floors. It can also divide wall space into separate areas to reinforce or define a proportional pattern for a building. A stringer course will often have a different bond pattern from the rest of the brick siding, As a practical matter stringer courses often present headers or rowlocks, so that the bricks in the next course will have a full brick to rest on.
Herringbone and other slanted patterns Where the bricks are not called upon to add significantly to the strength of a wall the bricks can be laid at an angle so that it is resting on a corner between two faces. This can create a herringbone pattern or a diamond pattern. Brick fill in half-timbered houses was an improvement over daub and wattle. Since the bricks were not structural a strong bond was not required. Decorative brick designs don't need to be as strong as regular bond if the design is small enough so that the rest of the wall can handle the support duties, or where there are structural elements, such as arches or timbers that relieve decorative area from carrying a lot of weight.
 A basket weave is both simple and sophisticated.
Functional aspects of brick siding One of the reasons that brick is seldom used for structural walls these days is the poor insulation properties of the traditional brick. While a brick wall can create a striking interior wall as well as a beautiful exterior wall, it won’t be a very warm wall.I once looked at a renovated brick house from the 1830’s. The owners had insulated the outside walls and then put up vinyl siding. They left the brick wall exposed on the inside. It was a terrible thing to do, but also necessary if they were to afford to heat it. 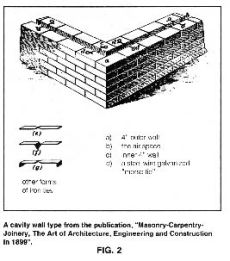 A guide to construction from 1899 shows a cavity wall with the same basic ties as we use today.
A cavity wall solves the moisture penetration problem. You might think that rain would just roll down the outside of a wall, but hairline cracks allows some moisture to penetrate the brick siding, and if a strong wind is blowing, sometime quite a bit of can penetrate. With a gap between the wythes moisture will roll down the interior face of the outer wythe, rather than penetrate to the house interior. At the bottom of the cavity flashing will span the gap to direct any moisture to weep holes that will allow water to exit from between the walls. In the 1970’s this was improved on the cavity wall by adding closed cell foam insulation to the interior wythe while still maintaining a small air gap between the exterior wythe and the foam. You can have R values as great as you achieve with other types of construction. This is the current state of the art in masonry construction.
Since this type of masonry requires no spanning bricks most of the current generation of brick siding uses a stretcher bond. We have gained tremendous technical advantages, but have lost much of the artistry that once characterized good brick work. Boring is not a requirement, its just cheaper and more convenient. The old bonds can be simulated with partial bricks, but with added costs. The cavity wall helps to explain the rise of the banal stretcher bond, but it doesn’t fully justify it. So I am putting in my request that anyone reading this article who is consider using brick siding investigate ways that they can make the brickwork beautiful. Yes, it will cost more, but beauty always comes with a price.
|
