Divine Proportions, Mathematics and the Proper Ceiling Height
Divine proportions speak the natural state of man and creation in a harmonious relationship with God. If all his creation is in harmony with him, and therefore in some kind of proportionate relationship, then mathematics should provide clues to that idea state.
To Pythagoras numbers seemed like a secret language for unraveling the mysteries of the world. That is my analogy, not his, but I think it is a Pythagorean idea to say that nature speaks in the language of mathematics. Pythagoras understood numbers like no one before him. In a time before we had computers, before we had calculus, before we had the terminology we use in mathematics today, before we even had zero, Pythagoras was fooling around with irrational numbers. He was the kid who always took home the mathematic prize at school, but spent much of his time explaining to his teacher how he had a better way of getting to the answer.
In Timaeus Plato describes the Pythagorean idea of a progression of numbers that God used as part of his creation.
These numbers are often expressed graphically as a sort of upside down V that looks like the Greek letter lamba. These are simply the numbers 2 and 3 squared and cubed.
We will recognize them as the basic building blocks of the proportion we have been looking at. Plato (on behalf of Pythagoras) goes on to talk about God filling in the gaps with a series of means. I won’t get into all of these numbers, and I am going to leave Pythagoras behind and jump to Palladio.
Divine Proportions: Palladio's Search for Perfect Rooms
 Palladio's Villa Almerico Capra
Palladio's Villa Almerico CapraI have described Palladio as being a practical architect. He uses Pythagoras’s ideas, but expresses them in terms useful to any architect. He tells us ways to use mathematics to identify good room proportions, proportions that are pleasing, divine proportions.
First of all he uses his understanding of music to develop seven proportions that he considered pleasing. They are:
- A circle (1:1)
- A square (1:1)
- A square and its diagonal (1:1.414…)
- A square plus a third (3:4)
- A square plus a half (2:3)
- A square plus two-thirds (3:5)
- A square plus itself (1:2)
There are two new proportions in this list, 3:5 and 1:1.414. For the first, I can only guess that changes in music theory led to its being accepted as harmonious. For the second we can jump back to Pythagoras for a moment. From geometry class you might remember the Pythagoran theorem for calculating the length of the diagonal of a rectangle, a squared plus b squared equals the diagonal squared. If you have rectangle with the sides of 3 and 4, then 3 squared (9) plus four squared (16) = (25) or five squared.
So the length of the diagonal is 5. You can do this for any rectangle but for the square the answer gets squirrely.
When Pythagoras tried to calculate the diagonal of the square, which is the square root of 2, he discovered that his calculations never ended. The actual number is 1.41421356… where all those little dots means it just goes on and on and on and…
Obviously this meant something special was up. We call these types of numbers, the ones that just go on, irrational numbers, because they cannot be expressed as a ratio. They can be expressed graphically, just draw a square and its diagonal. Easy-peasy. So we have a number that visually is simplicity itself, but numerically throws the old grey matter into a tailspin.
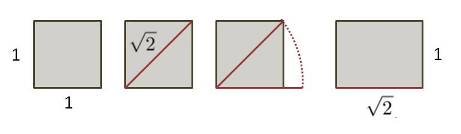
Well, architecture is visual, so Palladio accepts this ratio as one that will work just fine for his system, but Palladio has to take his system a step further if he is to build actual rooms. The rooms consist of squares and rectangle only on paper. In real life we have to deal with cubes. So how does one figure out the proper height of a ceiling for this wonderfully proportioned floor plan?
Palladio borrows from the idea of the mean, a type of average, in order to calculate his three room dimensions. He uses three different types of means to calculate that third dimension. He uses the arithmetic, geometric and harmonic means. Anyone of these three means will provide a room of divine proportions if applied to one of his seven ideal shapes (and presumably if applied to any of the other proportions we have discussed).
Most people are aware of the arithmetic mean. It is the number smack dab in the middle of two other numbers. The arithmetic mean of 8 and 10 is 9.
The geometric mean is trickier. It is the number where the ratio of the lower number to itself is the same as the ratio of itself to the larger number. The geometric mean of 4 and 9 is 6. The ratio of 4 to 6 is 2:3. The ratio of 6 to 9 is also 2:3.
The harmonic mean gives me a headache. I will start with an example. The harmonic mean of 6 and 12 is 8. Here is why. 8 is 1/3rd greater than 6. 8 is also 1/3rd smaller than 12. The general rule is (b-a)/a=(c-b)/c. In our example that equates to (8-6)/6=(12-8)/12.
To solve for the harmonic mean you take (a x b)/arithmetic mean or (a x b)/(a+b)/2, or (2xaxb)/(a+b). In our example that comes to 2x6x12/(6+12)=8.
Practical Applications of Divine Proportions
What does this mean from a practical standpoint? Well say you have an unfinished basement and you want to finish it out. Say the section that you want to finish is 15 feet by 24 feet. This fits the proportion of 10:16 (or 5:8), so the floor plan is classically proportioned. Now say you were going to install a drop ceiling to hide the ducts and wiring while still providing access. How high would you want that ceiling if you are to have a room built to divine proportions?
You need to look for a number smaller than 15’, so you would need to solve for the smaller number, which means 15 is going to be the mean and 24 the top number. What is the height if 15 is the arithmetic mean? 15 is the arithmetic mean of 6 and 24. A 6’ ceiling is just to short, so let us consider the geometric mean.
Since 15 is 5/8ths of 24 we just find 5/8th of 15, which is 9.375 feet. This is a workable number, assuming you have enough room under your floor joists.
We can solve for the harmonic mean with the formula a=cxb/(2c-b). This yields 10.91 feet. If you have the room this will work also.
If your floor plan did not work out to give you divine proportions for the floor then you could modify that shape with the framing of additional walls to create two rooms or a room plus storage behind one wall. From a practical standpoint it can be very difficult to make sure all of your rooms are well-proportioned and there may be functional reasons why you need a room to be a certain shape, but where you can do it there will be aesthetic rewards. Certainly rooms where you will spend a large amount of time should be well-proportioned where possible.
There is also the cost consideration. Building a house with multiple ceiling heights adds to the costs. We generally have a standard ceiling height, at least for a given floor. Yet consider what architect Christopher Alexander posits in his book A Pattern Language. Pattern 190 is Ceiling Height Variety. He states that A building in which all the ceiling heights are the same is virtually incapable of making people feel comfortable. So here you have another reason for creating rooms with divine proportions.
To Top of Page - Divine Proportions
To Proportions of Classical Orders
To Proportions and the Golden Ratio
Please!




New! Comments
Have your say about what you just read! Leave me a comment in the box below.