Proportions and Music in Architecture

Pitch Finds a Philosophy

The proportions of music are better understood today than in the past, but perhaps less appreciated. Today we can make music electronically, programming what specific frequencies and amplitudes we want to make. Back in the day, as in BC, they could only make music with instruments and they had no clear understanding of sound propagation. They had no way of measuring the sounds created and they had no clear system of notation for passing their music on to others. Yet the philosophical minds of the day recognized that there was regularity in music and, through observation, were able to develop theories of music that included an understanding or proportion.

While they had no direct way of measuring the sounds produced, they noticed that changing chord length, or drum size, or the even the weight dropped on an anvil, affected the pitch produced. What they discovered helped to shape their ideas of proportions. What I am about to describe is well outside my experience, so I will refer you elsewhere at the end of this article.

The musicians and philosophers noted that if you plucked a string with a length of 4 it gave one sound, and if you shortened that string to 3 and plucked it a different sound came out. They called the difference between the two a fourth. In other words, the difference in sound produced by two chords in the ratio of 3:4 is a fourth. If the two chords were in the ratio of 2:3 they called this a fifth. There is a really good reason for their nomenclature, and when I learn it I will teach it to you. In the meantime just shake your head up-and-down.

One term that you will recognize, even if you are musically dysfunctional like myself, is the term “octave”. This is the difference in sound for chords in the ratio of 1:2. In today’s musical system we recognize that notes that are an octave apart are the same note. Two C’s an octave apart will blend and sound appropriate together.

If you take all the numbers I have mentioned you come up with 1:2:3:4. The harmonies produced by music with these ratios seemed mystical and certainly important. Remember that they thought that God created all things to be in harmony with himself, so anything that bespoke of harmony was worthy of their attention and reflection.

On to the Renaissance

There was a lot more to their theory than this, but for our purposes it will get us to the early Renaissance where we meet a guy named Leon Battista Alberti, who was good at everything he did, and wrote about it as well. He probably got beat up a lot in school because he certainly knew all of the answers.

Alberti takes the idea of musical harmony a little further and clearly relates it to shape and to architecture.

He starts with the simple ratios already discussed 1:2, 2:3 and 3:4.

To get a second set of ratios he starts manipulating the above proportions. For instance, take the simple square. Find its fifth. Add the square to its fifth, then take the fifth of the new, larger shape and add it to its larger shape. Confused? The whole notation is confusing. I will state this another way that your modern ears may like better.

Take a square. To that square add a rectangle that is 1/2 as wide as that square. Now you have a new shape, which is a rectangle in the ratio of 2:3. Now take half of that rectangle and add it to the rectangle of 2:3. This longer rectangle will have the ratio of 4:9.

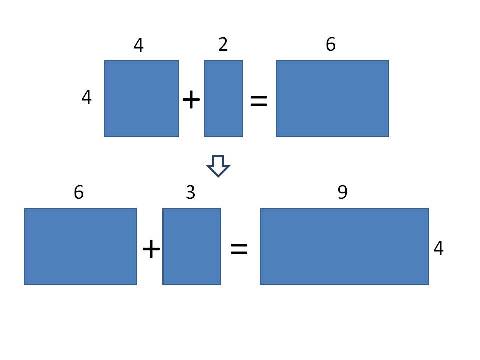
I won’t go into all of the combinations. The next one he looks at is as above, but he uses fourths instead of fifths to come up with a rectangle in the proportions of 9:16.

To these proportions he adds a third set of three shapes, in the proportions of 1:3,3:8 and 1:4. For a fuller explanation I suggest you go to Harmony and Proportion where John Boyd-Brent does a masterful job of explaining this information.

In summary, from music we have developed the following ratios as being naturally harmonious:

• 1:1 (I didn’t discuss this above, but it is his basic starting point)
• 2:3
• 3:4
• 1:2
• 4:9
• 9:16
• 1:3
• 3:8
• 1:4

Do you notice how the above are simply the basic numbers in our 1:2:3:4 progression, squared? For instance 2:3 squared is 2x2:3x3 or 4:16 or 1:4. The odd man out in that analysis is 3:8, which can only be reached by cubing 2 to get 8. Still, it suggests another way of getting to a set of pleasing proportions, mathematics. 

To Top of Page - Proportions and Music

To Divine Proportions - Proportions and Mathematics

To Perfect Proportions

To the Proportions of Man

To Proportions of Classical Orders

To Proportions and the Golden Ratio