The Golden Ratio

A Beautiful Rectangle

The Golden Ratio fits in with my discussion of proportions even though it is neither a proportion nor a ratio. Beloved by architects and artists and mathematicians it deserves the name Golden, but it belongs to a special class of numbers that cannot be expressed as a simple ratio.

In Vitruvian Man I discussed man's proportions and the Greek architects adaptations of a human metric. In my Proportions of Music article I covered how the Greeks understanding of musical pitch informed their thinking on architectural proportions. In Proportions of Mathematics I showed how classical architects used various measurements of the mean to develop proportions. In my The Classical Orders I showed how later architects used the proportions of Greek columns to define visual breakpoints in room interiors.

This is a negative of the Nashville Parthenon, a replica of the original Parthenon in Athens. The shot is from below, so it is distorted, but the face of the Parthenon fits the Golden Rectangle.

In all this I could never figure out how to bring up the Golden Ratio. It just never seemed to fit into the flow of my text. So here I introduce it, not as part of the historical narrative, but as a punctuation mark, my final word as I look back upon my handiwork.

While it is technically not a  ratio, an approximation of it can be expressed as a ratio, which means it can also be expressed as the proportion of two sides of a rectangle, and that rectangle is known as the Golden Rectangle. This famous ratio happens to be 1.61803…, and yes, those dots means it goes on forever, another irrational number that makes for wonderful proportions.

The Golden Rectangle has a reputation as being the most beautiful of all proportions. Ancient artists seem to have used it. Euclid wrote about it. It is mathematically fascinating and ends up making its way into various formulas and treatises. It shows up in various sciences, from biology to neurology.

The Geometry of Gold

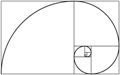
Here is why it came to the interest of Euclid. Like any rectangle, the Golden Rectangle can be divided into a square and another rectangle that makes up the remainder. However that remaining rectangle also happens to be a Golden Rectangle. There is no other ratio for which this is true. Of course this means that the smaller Golden Rectangle can also be broken into a square and an even smaller Golden Rectangle. You can keep on doing this forever, a geometric progression without end.

If you did do this forever and drew a curve through opposite corners of each of the squares you end up drawing a never-ending spiral, which looks a lot like a snail’s shell, or the shell of the chambered nautilus. Here is our first indication that the Golden Ratio is important in nature.

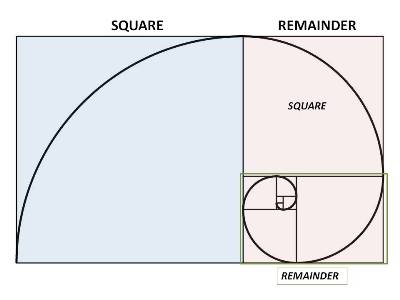A Golden Rectangle becomes a Golden Spiral

The Golden Ratio as a Series

While you can arrive at the Golden Ratio graphically, with just a protractor and a straight edge, you can also get there mathematically through the Fibonacci series. The Greeks can't claim this one, it came from an Italian of the Middle Ages, Leonardo Fibonacci. It is a simple arithmetic progression. Start with 0, then go to 1. Now add 0 and 1 to get 1. So now we have 0, 1, 1. Now take the last two numbers to get the next number, 3. From then on you follow that rule. Add the last two numbers to get the next number.

This gives you the series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

This series gets closer to our special ratio as it goes along. That is, if you take the current number and divide it by the previous number you get a ratio. The first set is 1 divided by 0, which yields a ratio of infinity. Then it is 2 divided by 1 or a ratio of 2. Then 3 divided by 2 to get 1.5. Each new step takes you a little closer to the Golden ratio. For instance 89 divided by 55 gives a ratio of 1.618182. It never ever reaches the Golden Ratio, because it is an irrational number and cannot be expressed as a ratio.

When Science is Golden

What you have is a special rectangle that has unique graphic properties, you can do crazy stuff with it mathematically, and it shows up in the darnedest places in nature. It is this hidden ubiquity that makes it so pleasing visually.

However there is some scientific support that the ratio may be hardwired into our biology, thus potentially making it more appealing to us. Volkmar and Harald Weiss, German scientists, analyzed psychometric data and concluded that the Golden Ratio forms the clock cycle of brain waves (whatever that means). This was later confirmed by neurobiologists.

A Famous Disciple

The Golden Rectangle had at least one vocal proponent among the early Modern masters. Le Corbusier had a love for proportion and supposedly based much of his work on the proportions of the Golden Rectangle. He even rejected the decimal system of measurement in favor of a system based on human scale and the Golden Rectangle.

You can make use of the Golden Ratio as you make use of the other proportions I have presented. I cannot swear that it is better than the others, but if Plato was right, and we are drawn to those things that are in harmony with the created world, then certainly a number with these unique properties should be among those that are considered in harmony with the world. 

Return to Perfect Proportions

Return to Architectural Concepts

Home - House Design